Quizze

    Kann durchaus sein! :D Mal gegentesten;


    Es gehört nur dir, aber andere Menschen nutzen es am Öftesten; Was mag das sein?

    I see the lights of the village

    gleam through the rain and the mist

    and a feeling of sadness comes o´er me

    that my soul cannot resist

    Haben wir also offenbar tatsächlich die selben Spiele gespielt - oder teilen uns wenigstens das Faible für Rätselfragen xD


    Von denen mir im Moment aber auch keine guten mehr einfallen. Deshalb blos noch ein kleines Gedankenspiel: Wenn ich in ein Boot steige, auf einen See hinaus fahre, und dann eine Münze ins Wasser werfe: Wird diese letzte Aktion den Pegelstand des Sees steigen, sinken oder gleich bleiben lassen?


    (Also alles im theoretischen Ideal betrachtet; Wers empirisch versuchen möchte, den will ich aber meinetwegen auch nicht aufhalten... ... :D)


    Und, weil das doch ein eher maues Rätsel ist, ein Tipp zu dem Streichholzrätsel von oben. Wenn ihr euch die Streichhölzer mal so vorstellt, was wäre die erste Idee, die euch zu vier Dreiecken und einem Quadrat einfiele? Denn das wär schonmal kein schlechter Start, wenn ihr von da an weiter überlegt!

    I see the lights of the village

    gleam through the rain and the mist

    and a feeling of sadness comes o´er me

    that my soul cannot resist

    Einmal editiert, zuletzt von Haggard ()

    Zitat von Haggard

    Haben wir also offenbar tatsächlich die selben Spiele gespielt - oder teilen uns wenigstens das Faible für Rätselfragen xD

    Von denen mir im Moment aber auch keine guten mehr einfallen.

    Davon habe ich noch jede Menge. :D


    Zitat von Haggard

    Wenn ich in ein Boot steige, auf einen See hinaus fahre, und dann eine Münze ins Wasser werfe: Wird diese letzte Aktion den Pegelstand des Sees steigen, sinken oder gleich bleiben lassen?

    Ich würde sagen es bleibt gleich, da die Münze sich ja schon im Boot befindet und dadurch schon der Pegelstand beeinflusst wird. :onion-confused:


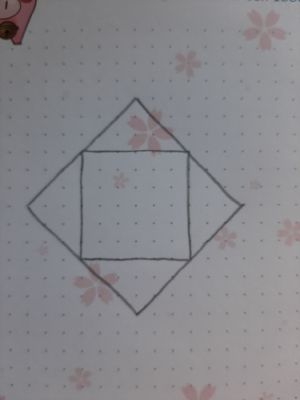
    Bin nicht sicher, ob das stimmt, denn streng genommen wären die äußeren Streichhölzer ja länger als die innen.

    2B and 9S (gif) : r/nier

    "The time I was able to spend with you.

    It was like memories of pure light. Thank you..."

    Was das Rätsel mit dem Boot und der Münze angeht bist du schon auf dem richtigen Weg mit dem Gedanken der Verdrängung; Versuch dir mal den See kleiner und die Münze grösser zu denken - ich wette, du kommst noch dahinter!


    Und das Streichholzrätsel, ja, auch hier muss ich ebenso streng zu dir sein, wie mans zu mir war! :D Streichhölzer sind in der Regel alle gleich lang, und dann würde diese Lösung leider nicht funktionieren. Aber auch hier... ich schrieb, es müssen vier Dreiecke zu erkennen sein, und es ergibt sich aus der Lösung, dass diese vier auch recht symetrisch sind. Blos: Das diese vier Dreiecke auch gleichschenkelig sein müssen, davon war ja nicht die Rede... ^^

    I see the lights of the village

    gleam through the rain and the mist

    and a feeling of sadness comes o´er me

    that my soul cannot resist

    Ach ja, wie dumm. :facepalm: Wenn die Münze sich im Boot befindet zählt ihr Gewicht natürlich zu dem des Bootes und da das Boot mehr Volumen hat wird auch mehr Wasser verdrängt, als wenn nur die Münze im See liegen würde. Demnach müsste der Wasserstand sinken.


    2B and 9S (gif) : r/nier

    "The time I was able to spend with you.

    It was like memories of pure light. Thank you..."

    Zum Einen: Ganz Recht, der Umstand, dass eine Münze im Wasser untergeht verrät ja, dass ihre spezifische Dichte höher liegt als die von Wasser. Solange sie sich im Boot befindet wird der Pegelstand des Sees (durch Verdrängung) von ihrem Gewicht beeinflusst, nicht aber von ihrem Volumen. Wenn man sie über Bord wirft ändert sich das, denn nun zählt ihr Gewicht nicht mehr, nur noch ihr Volumen -> Der Pegelstand sinkt.


    Und auch das Streichholzrätsel ist gemäss der Aufgabenstellung gelöst! Ich hätte aber auch das hier gelten lassen. (Wobei man gucken müsste, welche von beiden Lösungen das kleinere Gefriemel wär! :D)

    I see the lights of the village

    gleam through the rain and the mist

    and a feeling of sadness comes o´er me

    that my soul cannot resist

    Dann kommt jetzt das nächste RPG Rätsel. :D


    Ein Teil eines Vogels,

    aber nur auf Erden.

    Kann schwimmen im Wasser,

    ohne nass zu werden.

    Was ist das?

    2B and 9S (gif) : r/nier

    "The time I was able to spend with you.

    It was like memories of pure light. Thank you..."

    Zitat von James

    Ich fand das nicht einfach. :(

    Ok, wenn die doch nicht zu einfach sind, dann mach ich damit weiter. :)


    Welches Wort spricht auch der größte der sterblichen Weisen falsch aus?

    2B and 9S (gif) : r/nier

    "The time I was able to spend with you.

    It was like memories of pure light. Thank you..."

    Ja ok, ist vielleicht etwas altertümlich ausgedrückt. :eo-sweat:

    Anders ausgedrückt: Welches Wort spricht auch der klügste Mensch falsch aus?

    2B and 9S (gif) : r/nier

    "The time I was able to spend with you.

    It was like memories of pure light. Thank you..."

    Haha :muha:

    Diesmal hats aber länger gedauert und ich musste den Satz mehrmals lesen. Okay, jetzt will ich aber mal selbst ran, hab was schwierigeres für euch raus gesucht. Zumindest hoffe ich, dass es schwer ist.


    Ihr habt ein Haus geerbt. Ein schönes großes Herrenhaus, von Wald umgeben und mit Blick auf einen großen See. Nun inspiziert ihr es und als ihr im Keller den Sicherungskasten erblickt müsst ihr feststellen, dass kein einziger Schalter für die Lichter beschriftet ist. Ihr habt jetzt also 200 unbeschriftete Schalter und möchtet diese den zugehörigen Lampen zuteilen, pro Lampe ein Schalter. Ihr möchtet aber nicht 200 mal hoch und runter laufen um zu sehen welcher Schalter zu welcher Lampe gehört, also müsst ihr euch etwas klügeres einfallen lassen.


    Wie oft müsst ihr minimal in den Keller gehen um herauszufinden welcher Schalter zu welcher Lampe gehört? (Mit Erklärung bitte)

    Sei N die Anzahl der Lichtschalter, wir teilen N in n verschiedene Gruppen an Lichtschaltern die wir je Gruppe gleichzeitig an haben und notieren uns welche Gruppe welche Lampen einschaltet. Danach werden wir im Keller alle Lichtschalter ausschalten und nur N/n Schalter aus immer unterschiedlichen Gruppen einschalten. Wenn wir jetzt gucken gehen, können wir aus den Lampen die jetzt an sind und unseren Notizen sehen, welcher Lichtschalter welche Lampe angeschaltet hat.


    Nun ein bisschen Mathe:

    wir wollen die Funktion f(n) = n+N/n minimieren. (Wir sind n mal also für jede Gruppe hoch und runter + wir haben in einer Gruppe N/n Lichtschalter müssen also nochmal N/n mal hoch und runter)

    Dazu suchen wir uns den Minimalpunkt indem wir die Ableitung nehmen und auf Null setzen.

    f'(n) = 1 - N/n² = 0
    => N/n² = 1

    => N = n²

    sqrt(N) = n


    dann setzen wir die gegebenen N auf 200 abzüglich 4 damit es aufgeht: sqrt(196) = 14

    und setzen dies wiederrum in f ein f(sqrt(196)) = 28

    dann haben noch einen Rest von vier den wir einfach in 4 zufällige Gruppen aufgeteilt hatten und dafür einmal in der Aufteilung und am Ende einen Schritt mehr gemacht haben!

    Also gehen wir 30 mal in den Keller!